6.3.2 映像符号化技術
映像の圧縮符号化を行う目的は,元の映像に含まれている重要な情報を保存しながら,映像を構成するその他の冗長な情報を多少削除しても元の画質を損なわないような工夫をして,できるだけ少ないディジタル符号量でその画像を表現することにあります.このため符号化するということは,冗長度除去と言われたり圧縮と言われたりします.
音声,映像に関わらず言えることですが,圧縮符号化の本質は,元の信号にほんの少し歪みを許し,表現に必要なビット量を大幅に減らす処理だということです.通常歪みを小さくしようとすればビット量が増えます.従って,符号化歪み,すなわち復号したときの品質を問わなければ,いくらでも圧縮できることになります.
なお,目的によってはロスレス符号化と呼ばれる歪み零の圧縮符号化技術もありますが(例えば可変長符号化だけを用いる),一般に大幅な圧縮は期待できません.
映像信号の圧縮符号化では,主に次のような方法が利用されます.
- 信号に含まれている冗長な部分を除去する -- ある画素の値は,周辺の画素の値に近い.画素のグループが示すパターンを見ると,なだらかな変化のものが多い.フレーム間で見ると同じ画像が続いたり,動きに応じて場所は変わるが同じようなパターンが現れる.
- モールス符号と同じように,よく出てくる信号は短い符号で表現して統計的冗長度を除く.
- 人間の視覚特性を利用する -- 人間の目は,複雑なパターンには感度が低い(正確に再現されていなくてもわからない).
なお音声と異なり画像には一般的な情報の発生機構は存在しません.従って映像符号化では,CELP音声符号化のような生成機構モデルに基づいて効率的に圧縮符号化する技術はありません.
この後,符号化技術を歴史的に俯瞰し,個々の符号化技術について詳しく説明します[6-32].
1) 映像圧縮符号化技術の発展
まず映像圧縮符号化技術の発展を,時代を追って歴史的に概観しますと,図6-31のようになります.ここでは,長年にわたり沢山の人が関わった研究開発成果の中から,変革をもたらした技術を選んで記しています.
映像圧縮符号化技術には,図6-31からわかるように,大きくは,
- 映像を構成する個々の画素を処理単位とする画素ベースの予測符号化技術
- 映像を構成する画素のブロックを処理の単位とするブロック・ベースの変換符号化あるいはベクトル量子化技術
の2つの流れがあり,現代の映像圧縮符号化ではこの両者を組み合わせたハイブリッド符号化が枠組みとなっています.可変長符号化技術はこれら全てに共通に使われます.
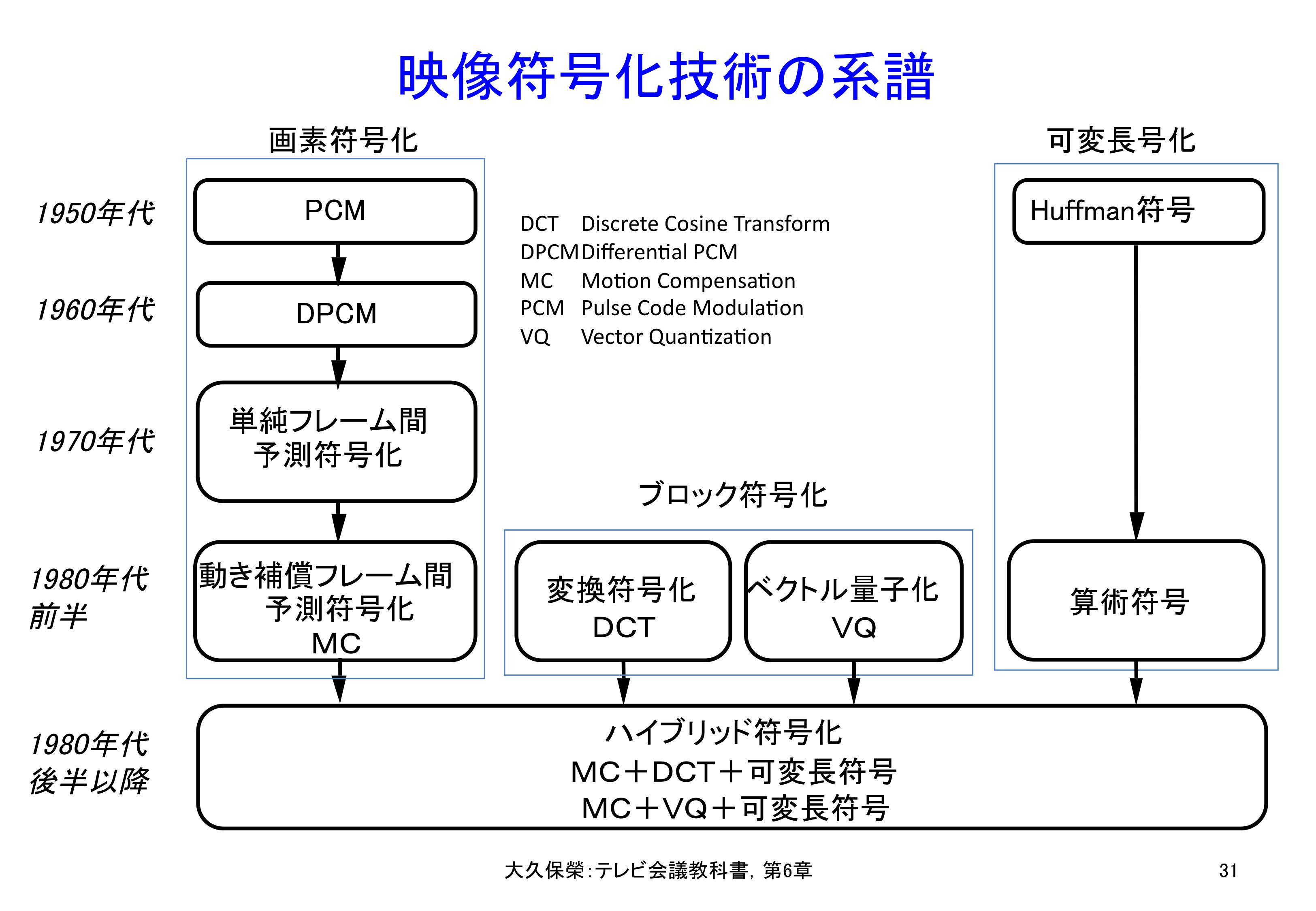
映像符号化技術は,大きく分けて画素ベースの符号化技術である予測とブロックベースの符号化である変換(あるいはベクトル量子化)の流れで捉えることができます.この図では変革をもたらした技術要素を示しています.1980年代後半以降は,両者を組み合わせたハイブリッド符号化が枠組みとして確立しています.
2) PCM
PCM (Pulse Code Modulation)は,アナログ信号をディジタル表現する圧縮符号化の第一歩です.本章第6.1節で述べましたように,標本化と量子化の処理を行います.
テレビ信号にPCMを適用した最初の論文は,1951年,アメリカAT&Tのグッダール氏によって発表されています[6-33].これが映像圧縮符号化時代の幕開けです.
標本化間隔は,第6.1節で説明しましたようにナイキスト(Nyquist)の定理から明らかですので,量子化をどの程度細かく行えばよいかが問題です.モノクロの画像信号の場合は,黒から白の間の灰色で表され,これを表す信号レベルの代表値の数が少なすぎると復号した画像に地図の等高線のような偽輪郭(ぎりんかく.現実には存在しないはずなのに表示される擬似的な境界線.英語ではfalse contouring)が現れます.代表値の数を多くするにつれて画像はきれいになりますが,ディジタル符号の量が増えていきます.従来のアナログテレビ(SDTV)映像や高精細テレビ(HDTV)映像に対しては,8ビットの量子化を行えば実用的であることがわかっています.
3) DPCM
圧縮技術の面で最初に変革をもたらしたのは,PCM信号をそのまま送るのではなく,予測誤差を送るDPCM(Differential PCM,差分PCM)です[6-34].その構成と動作をPCMと比較し,図6-32に示します.最も単純な予測の方法は,現在の画素値(例えば図6-32の2番目では6)は1つ前の画素値と同じ(例えば図6-32の1番目の5)である,とすることです.図6-32の信号の場合,PCMとDPCM(Differential PCM,差分PCM)では,c)に示す値を送ることになります.
最初の画素に対しては1つ前の画素が存在せず,差分の取りようがありませんので,1つ前の画素値は0であったとしています.したがって,DPCMの最初の値は,0とPCMの5の差分である+5から始めることになります.
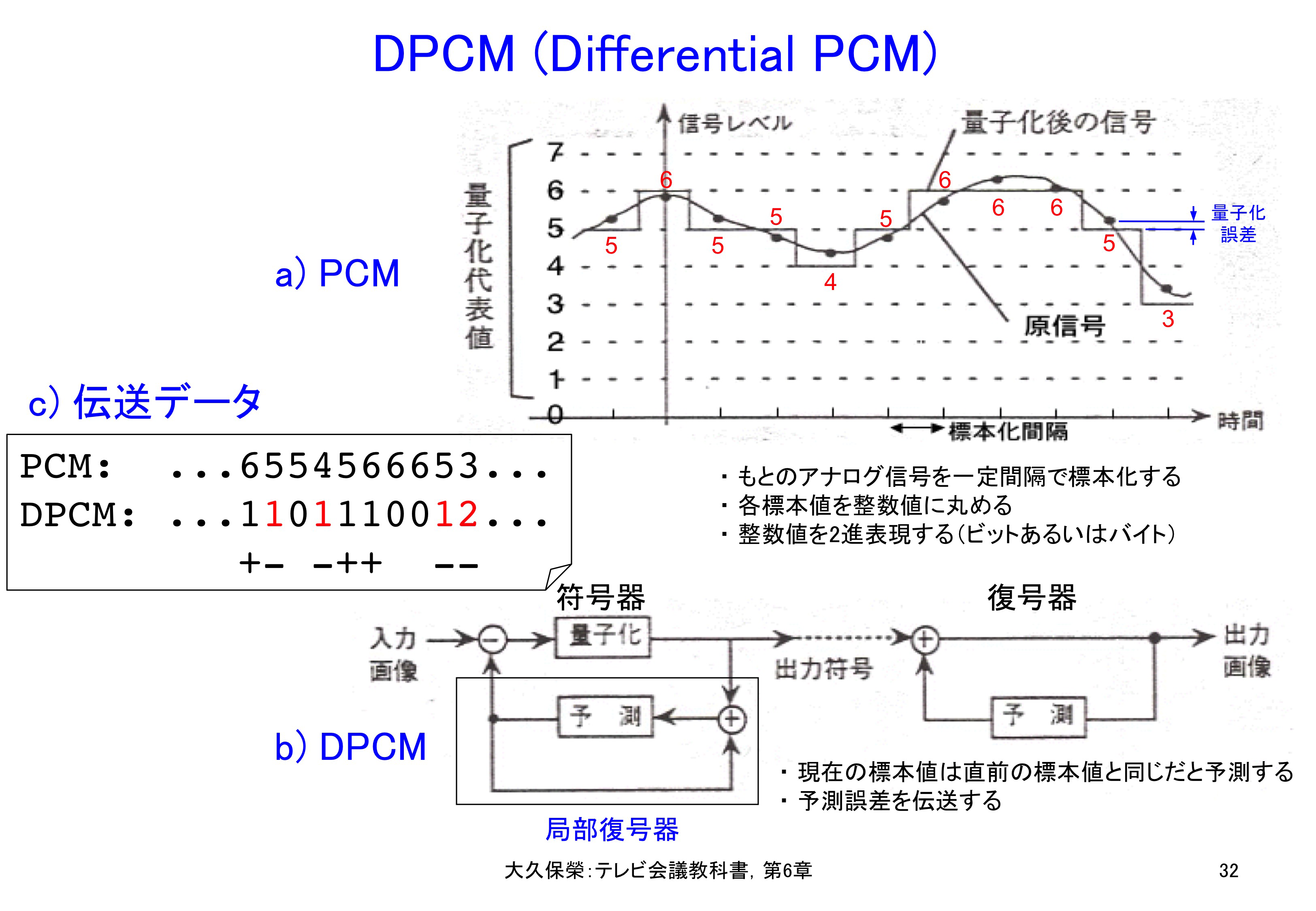
a)は基準となるPCMの標本化,量子化の処理を,b)はDPCM予測符号化方式の構成を示します.DPCM符号器では予測誤差を量子化して送り出し,復号器では復号済みの画素に送られてきた予測誤差を加えてもとの映像を再現します.c)はPCMとDPCMの符号化結果で,見た目にもDPCMの情報量が減っていることがわかります.
図6-32から,一見して,DPCM信号の方がPCM信号よりも少ない情報量で表現できそうなことがわかります.DPCM復号器では,すでに送信されてきた復号済みの画素値(この場合,最初に送られてきた「5」)に,順次送られてくる予測誤差,
+1, -1, 0, -1, +1, +1, ...
を加えていくことによって,元のPCM信号を再現することができます.
図6-33に,実際のQCIF画像(QCIFは縦横画素数をそれぞれCIFの半分にしたフォーマット)について,原画像と画素間の差分値を画像にして示します.
この画像はSusieと呼ばれ,国際標準化作業で用いられた試験画像の一つで,電話のハンドセットを持って顔を動かす場面です.差分値は,0を中心に+,−の両側の値を取りますので,画面上では差分値0は灰色に相当する形で表示されています.図6-33では,そのQCIF画面のY(輝度)成分について,PCM画素値とDPCM予測誤差値の振幅分布を合わせて示しています.
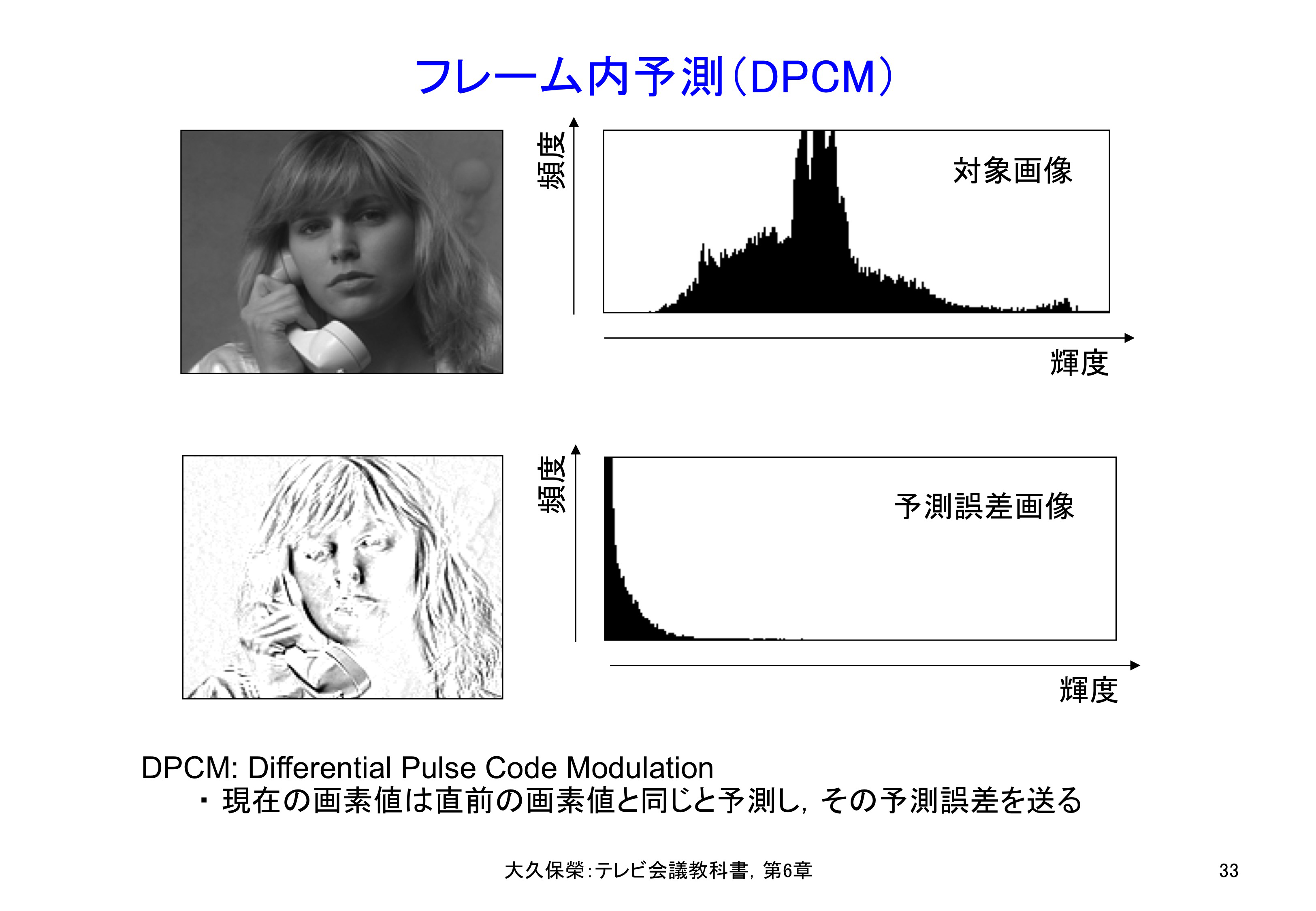
ITU-Rで定めた映像符号化試験画像の一つSusieの原画像と,左隣り画素から予測(フレーム内予測)したときの誤差画像です.それぞれの信号の振幅分布も一緒に示しています.予測により,冗長な情報が除かれている様子がわかります.
図6-33で明らかなように,予測誤差画像は線画のようになっていて大半が0付近の誤差値であること,予測誤差振幅分布は0に集中する指数分布になっていることから,予測により圧縮の効果が得られることがわかります.情報理論では,一般に偏った振幅分布であるほど,その信号の持つ情報量は少ないことが知られています.
予測に用いる画素は,これから送ろうとする画素より時間的に前のものであれば,直前の画素に限ることなく,複数個でもかまいません.一般に過去のデータが多ければ多いほど正確な予測ができることは,野球打者が打席に立つ場合と同じです.
そこで,すでに符号化が終わっている画素に重み付けした値(例えばこれから符号化する画素の左隣と真上の画素は既に符号化が終わっているので,これらに各1/2の重みを付ける)を用いるのが一般化した予測です.
予測符号化の符号器と復号器の構成を図6-32に示しました.符号器の構成要素として復号器と同じものが含まれています(図6-32では予測器と加算器からなる).局部復号器と呼ばれますが,これによって送信側で意図した信号が受信側で得られるようになっています.予測に用いる画素が,符号化しようとする画素と同じフレーム(画面)に属する場合はフレーム内予測,異なるフレームに属する場合はフレーム間予測と区別しています.
4) 単純フレーム間予測符号化
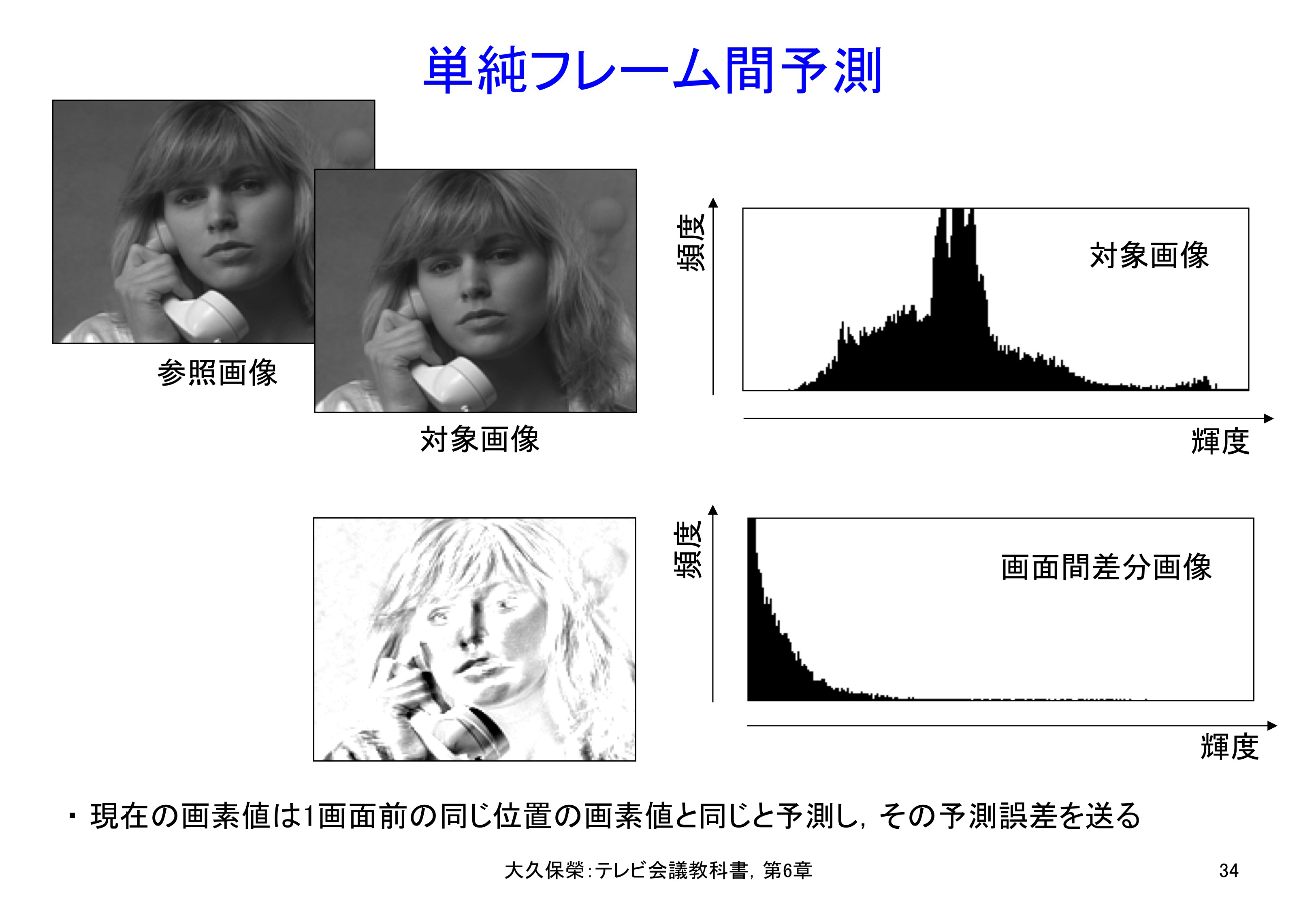
テレビ会議のような被写体の動きが比較的小さいシーンを撮した映像では,隣り合ったフレームはほとんど同じになります.
そこで,前述したDPCMの方法をフレーム間に適用すれば高い圧縮効果を得ることが期待できます.このためには,1フレーム(33.3 ms = 1/30秒)前の画像信号を必要としますが,これは大容量のメモリがあってはじめて可能になります.画像のフレーム・メモリが実用的になったのは1970年代で,それとともにフレーム間符号化装置が実現できるようになり,リアルタイムの画像伝送に用いられるようになりました[6-35].
前出の図6-33で示した試験画像Susieについて,2つフレーム間の差分画像とその振幅分布を図6-34に示します.前出の図6-33の隣接画素間差分と同様,DPCMの効果が得られていることがわかります.
5) 動き補償フレーム間予測符号化
フレーム間予測符号化は,動きの少ない画像に対しては効果的な圧縮方法ですが,大きな動きが発生すると2つのフレーム間の類似性がなくなり,差分を取るとかえって情報量が増えてしまう場合もあります.このことを模式的に図6-35に示します.
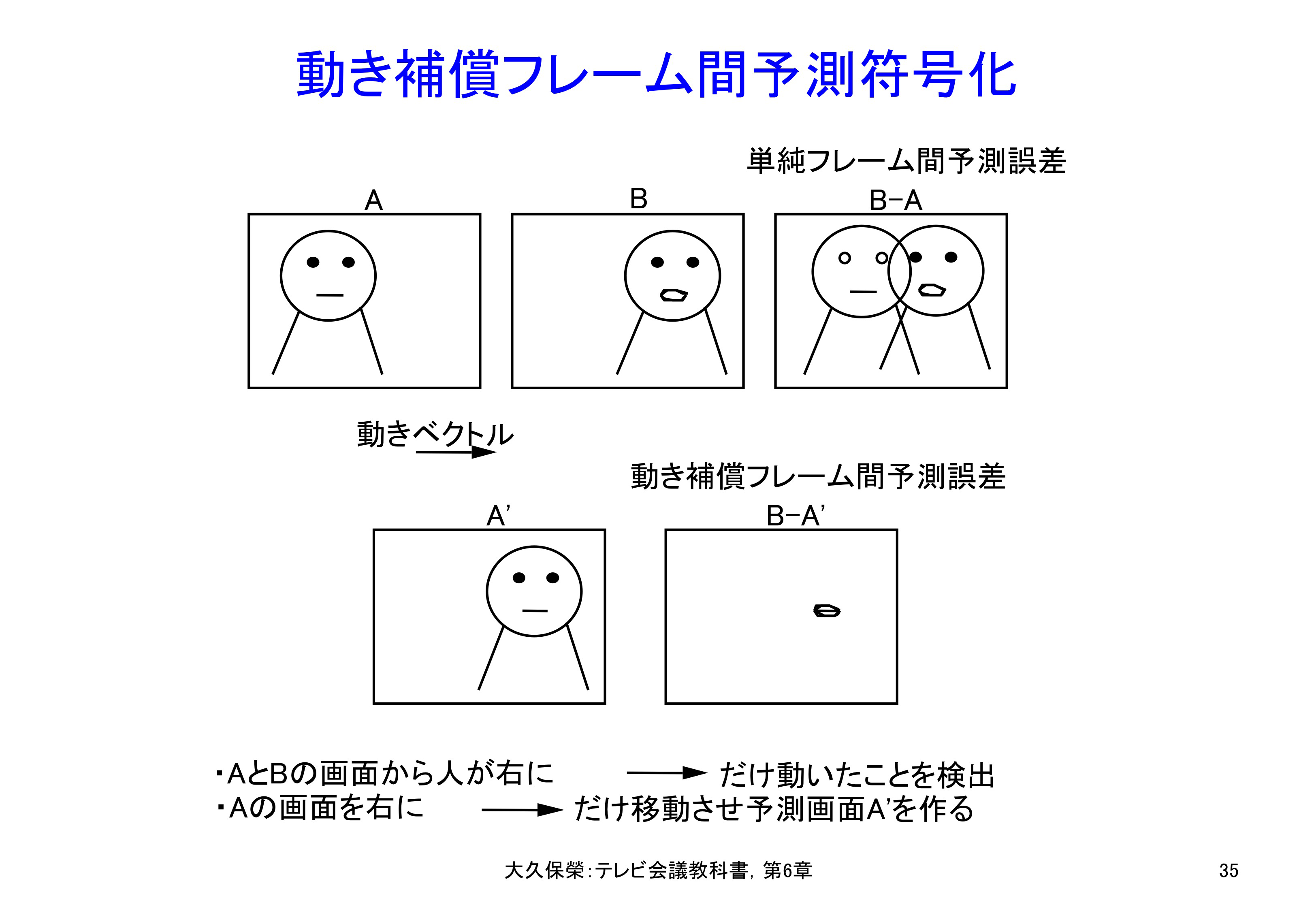
符号化すべき画面の中の被写体が前の画面からどれだけ動いたかを検出し,それによって予測画面を作るのが動き補償フレーム間予測です.この図ではその原理を模式的に説明しています.Bの画面ではAの画面に比べ被写体の人が右に動き話し始めたことを想定しています.単純な前画面からの予測では予測によりかえって送るべき情報が増えてしまいますが,動き補償フレーム間予測により送るべき情報が激減する様子を示しています.
図6-35における最初のフレームAの被写体は,次のフレームBで右方向に移動し,口を開いて話し始めた場面です.このまま2つの画面の差分をとると図6-35右のB - A(単純フレーム間予測誤差)のように二重写しとなり,これを符号化しても圧縮効果は得られません.
しかし,フレームAの被写体が右方向にどれだけ動いたかの情報(動きベクトル)があれば,これを用いて予測画面A'を作ることができ,そのうえで動き補償フレーム間予測誤差B - A'を求めれば非常に効果的なことがわかります.この技術を,動き補償フレーム間予測と呼びます.これは,映像圧縮符号化に大きな変革をもたらした技術の一つです[6-36].動きベクトルを探し求める処理には多くの演算を必要とするため,実用的になったのは1980年代初め頃からです.
試験画像Susieについて,予測誤差画面とその信号振幅分布を図6-36に示します.予測誤差画面では,ほとんど平坦になっていて予測誤差が0に近いことがわかりますし,振幅分布も図6-33のフレーム内予測や図6-34の単純フレーム間予測の場合と比べ,一層0の近辺に集中しています.
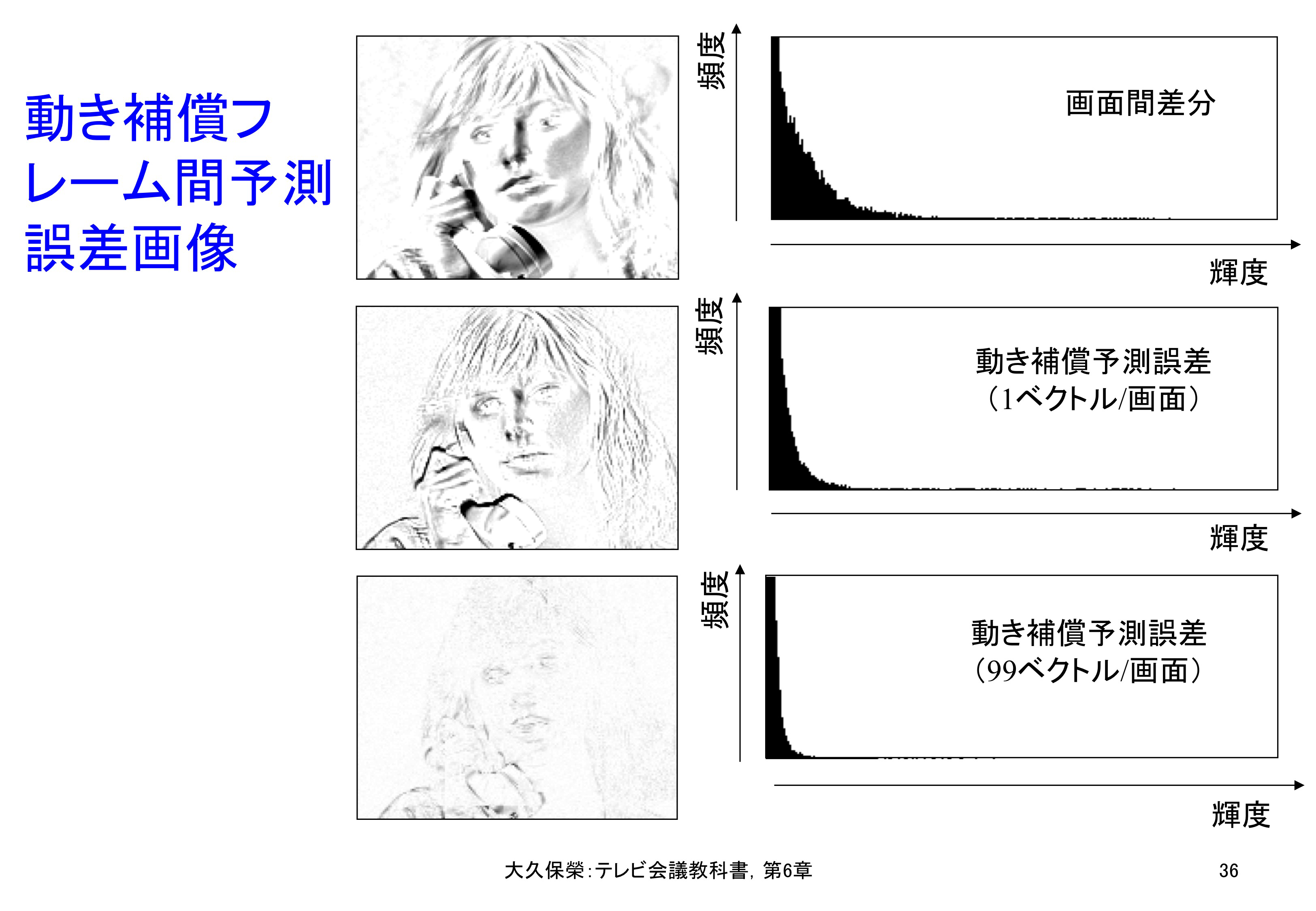
試験画像Susieにより,動き補償フレーム間予測の効果を示しています.上段は単純なフレーム間予測,中段は176x144画素からなる画面全体に1個の動きベクトル,画面全体では11x9=99個の動きベクトルを用いた場合の動き補償フレーム間予測誤差,下段は16x16画素ブロック毎に1個の動きベクトルを用いた場合の動き補償フレーム間予測誤差を示しています.下段の予測誤差画像,振幅分布から動き補償の効果を見ることができます.
実際の動き補償フレーム間予測では,1つの画面を小さなブロック(例えば16画素×16ライン)に区切ってそのブロックごとに動きベクトルを定義します.動きベクトルは,符号化しようとするブロックに最も似ているブロックを,符号化済み画像の中を探索して見つけます[6-37].この動きベクトル検出の方法はブロック・マッチング法と呼ばれます.相手に伝送される信号は,予測誤差と動きベクトルの情報です.ブロックの大きさを小さくするにつれて,予測は当たりやすくなり予測誤差情報は減っていきますが,動きベクトル情報が増えますので,適当なブロックの大きさが存在します.
動き補償フレーム間予測の拡張として,MPEG-1標準[6-38]では過去のフレームを参照して現在のフレームの動き補償をするだけでなく,現在のフレームに続く未来のフレームも参照して動き補償を行う方法が採り入れられました.
これは双方向動き補償フレーム間予測といわれる技術です.図6-37にその原理を示します.第nフレームに対し,第(n−1)フレームからの順方向動きベクトルと第(n+1)フレームからの逆方向動き補償ベクトルを用いて予測を行います.符号化効率向上の理由は,2つの動き補償ベクトルからの予測値を平均することによって最終的な予測値としますので,より正確な位置に予測画面を作り出せる,平均の動作が予測画面の符号化雑音除去(符号化結果は元の画像と比べれば符号化歪み,すなわち符号化雑音を含む)に役立っている,などが挙げられています.
双方向動き補償予測は,1990年代初めに実用的となった技術です.
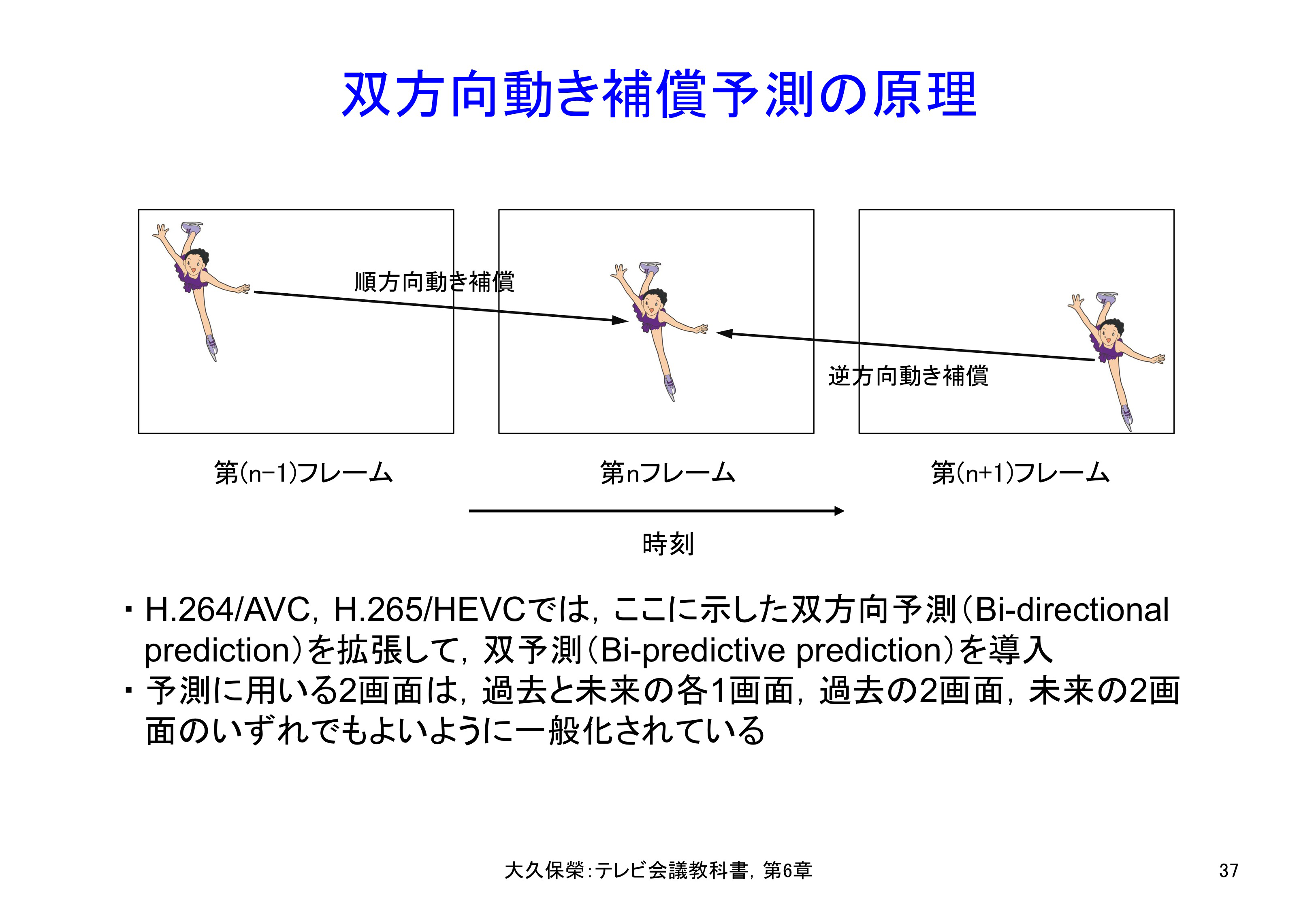
過去の画面から現在の画面を順方向に予測することに加え,未来の画面から現在の画面を逆方向に予測することにより,一層正確な予測が可能になります.ただし,入力画面を一旦フレームメモリに蓄積し符号化すべき画面の順序を入れ替えなければなりませんので,符号化に伴う遅延は増加します.
6) 変換符号化
変換符号化は,画像を画素のレベル値ではなく,周波数成分に分解して表現することにより,画像の性質(例えば図6-24に示した周波数スペクトラム)をより利用し易くする技術です.変換方法の一つがDCT(Discrete Cosine Transform, 離散コサイン変換)[6-39]で,1980年代になって実用的となった圧縮符号化技術です.それまでの画素単位の符号化ではなく,16画素x16ライン(= 256画素),8画素x8ライン(= 64画素)など多数の画素を集めてブロックとし,そのブロック単位で圧縮符号化処理を行うブロック符号化技術の一つです.画素をブロック化することによって集合的な冗長度を除くことができるため,圧縮符号化効率を高めることができます.
図6-38に8画素x8ライン(=64画素)でブロックを構成する場合について,
- 信画像の画素領域の表現f(i,j)を周波数領域の表現F(u,v)に変換するFDCT(Forward DCT,順方向変換式)
- 逆に周波数領域の表現F(u,v)から画素領域の表現f(i,j)に戻すIDCT(Inverse DCT,逆方向変換式)
を示します.ここで,(i,j)は画素の平面上での位置を,(u,v)は2次元周波数を示しています.

FDCTでは,ブロック内画素位置(i,j)と目的とする2次元周波数(u,v)で決まるコサイン関数の値とその位置の画素値を掛け,その結果を64個の画素について足し合わせて周波数(u,v)のDCT係数値を算出します.IDCTでは,逆にDCT係数の2次元周波数(u,v)と目的とする画素位置(i,j)で決まるコサイン関数の値とその周波数のDCT係数値を掛け,その結果を64個の2次元周波数について足し合わせて画素位置(i,j)の画素値を算出します.DCTでは無理数であるコサイン関数値や多数の積和処理が必要ですので,演算処理量が大きくなります.
DCTは,元の画像を2次元の周波数成分に分解する処理であり,そのときの周波数成分は図6-39に示します基底画像(8x8画素を周波数分解するので64個の基本パターン画像からなる)で表されます.左上が水平方向にも垂直方向にも低い周波数成分に対応し,右下が高い周波数成分に対応します.
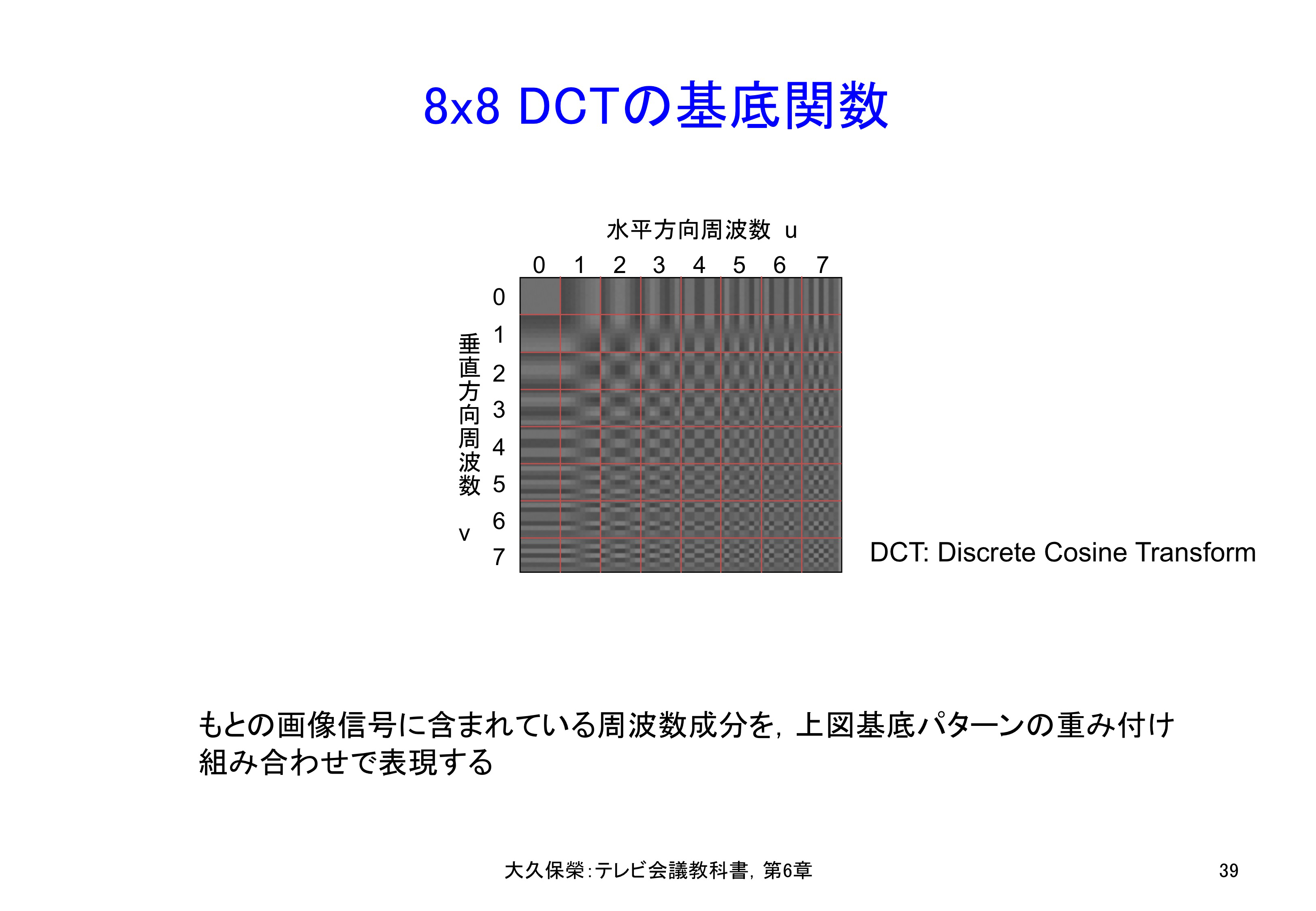
2次元の周波数成分64個をパターンにして示しています.左上の直流成分から右下の最高周波数成分まで,右および下にゆくほど高い周波数成分となり,複雑なパターンとなります.自然界でみかけるパターンは左上のものが多く,右下にゆくほどまれであることが,DCTで圧縮効果が得られる理由です.また視覚的に高い周波数成分に対する誤差の感度は低いことが,もう一つの理由です.
DCT変換を行うことは,元の画素ブロックに含まれているこれら基底成分(64個の基本パターン成分)それぞれの大きさを求めていることになります.この各基本パターン成分の大きさがDCT係数といわれるものです.
DCTは,単に元の画像信号を周波数成分で表現するための変換です.従って周波数成分から,逆変換によって元の画像信号を完全に復元できます.すなわち,DCTは画像の表現方法を変えているだけで,元の画像に含まれる情報は,冗長な情報も含め,すべて保存されています.試験画像Susieを8x8 DCT変換して得られた画像と,周波数成分F(u,v)値の分布を図6-40に示します.元の画像やその振幅分布に比べ,DCT係数値は0近辺の値に集中していることがわかります.
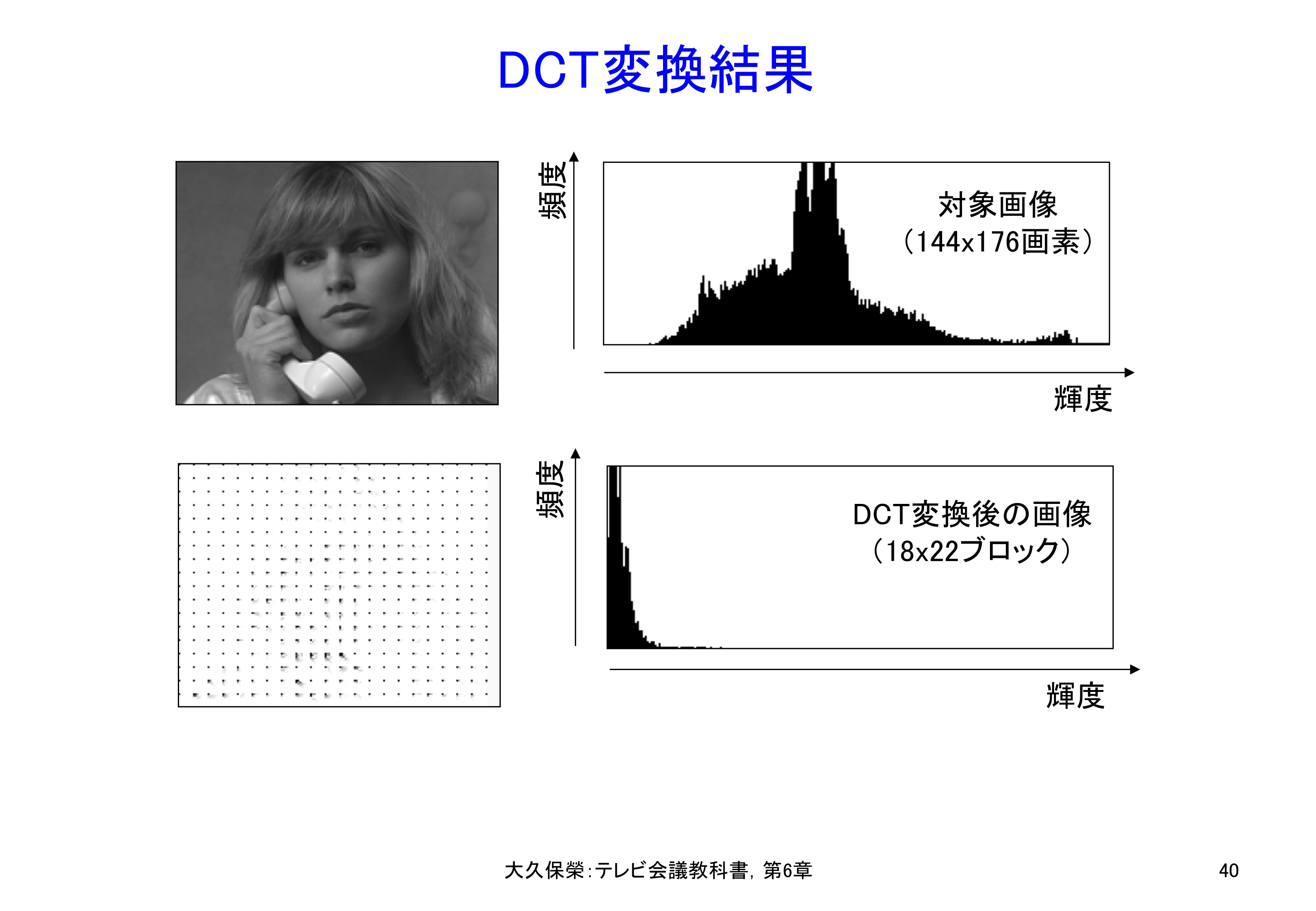
試験画像Susieを8x8画素のブロックに分け,各ブロックをDCT変換した結果の画像とDCT係数値の振幅分布です.DCT変換により効率的な符号化のできることが見て取れます.
この画像の中の特定の8x8画素ブロックについて,画素の値とDCT係数の値を図6-41に示します.DCT変換によって,DCT係数が左側(直流成分近辺)に偏って分布していますので,圧縮の可能性の高いことが見てとれます.
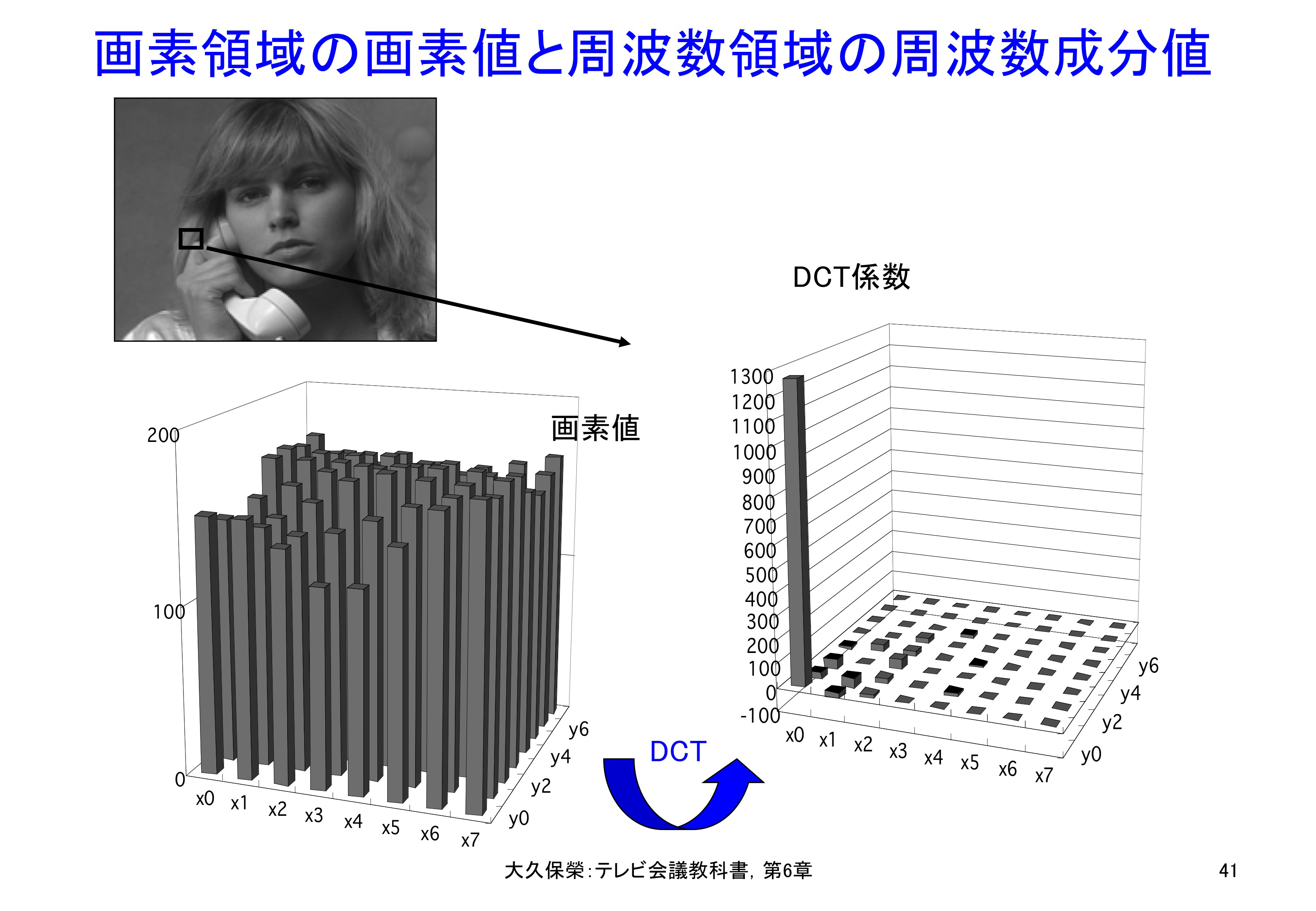
試験画像Susieの特定位置の8x8画素ブロックについて,画素値とそれをDCT変換して得られる係数値の様子を示します.高い周波数成分はほとんど零であり,少数の低周波成分でもとの画素ブロックを表すことができます.
7) ベクトル量子化
ブロック単位の符号化方法には,DCTの他に1980年代後半に着目されたベクトル量子化(VQ:Vector Quantization)技術があります.ここでベクトルとは複数の値で定義される量で,画像符号化では複数画素の値で定義されます.複数個の画素からなる画像のパターンは,すべてが均等に出現するわけではなく,画像の種類によって頻繁に現れるパターンと,まれにしか現れないパターンがあります.そこで,代表的な画像のパターン集(コードブックと呼ばれます)を定めておき,コードブックの中から符号化すべきブロックに最も近い代表的な画像パターン(コード)の1つを選択します.送るべき信号は,元の画素値ではなく,この代表的な画像パターンを表す番号(コード番号)です.
最も近い画像パターンを選ぶことは,図6-2で説明しました画像信号の量子化を複数画素(その集まりがベクトルを構成する)に拡張したものであることから,ベクトル量子化と呼ばれます.通常の量子化は,1個の画素値に対し量子化代表値(代表的なパターンに相当)の中から最も近いものを選ぶ処理ですから,ベクトル量子化はそれを複数画素に拡張した,ということになります.少ないコード数のコードブックで,元の画像が表現できれば,圧縮の効果が得られることになります.
その原理を模式的に表しますと図6-42のようになります.ここでは,白黒2値の画素を4x4個のブロックにしてベクトル量子化する例を示しています.
動き補償フレーム間予測とベクトル量子化を組み合わせた符号化装置が製品化されたことはありますが,これまでのところ,ベクトル量子化を採り入れた映像圧縮符号化標準はありません.今後の検討対象です.

ベクトル量子化は,元の複数画素からなるブロックをそれに最も近い代表的なパターン(コードブック)の一つに対応づける処理です.この図では2番目のコードが入力ブロックに近いことからその番号2を伝送します.入力ブロックのパターンと#2のコードが示すパターンとでは違いがあり,これが量子化誤差になります.
8) ハイブリッド符号化
予測と変換の双方を用いる映像符号化方式[6-40]はハイブリッド符号化と呼ばれ,1980年代後半以降現在まで,映像符号化標準の枠組みとなっています.動き補償フレーム間予測で動画像情報の持つ時間方向の冗長度を除き,DCTによって予測誤差に残存する空間方向の冗長度を除きます.その符号器構成を図6-43に示します.
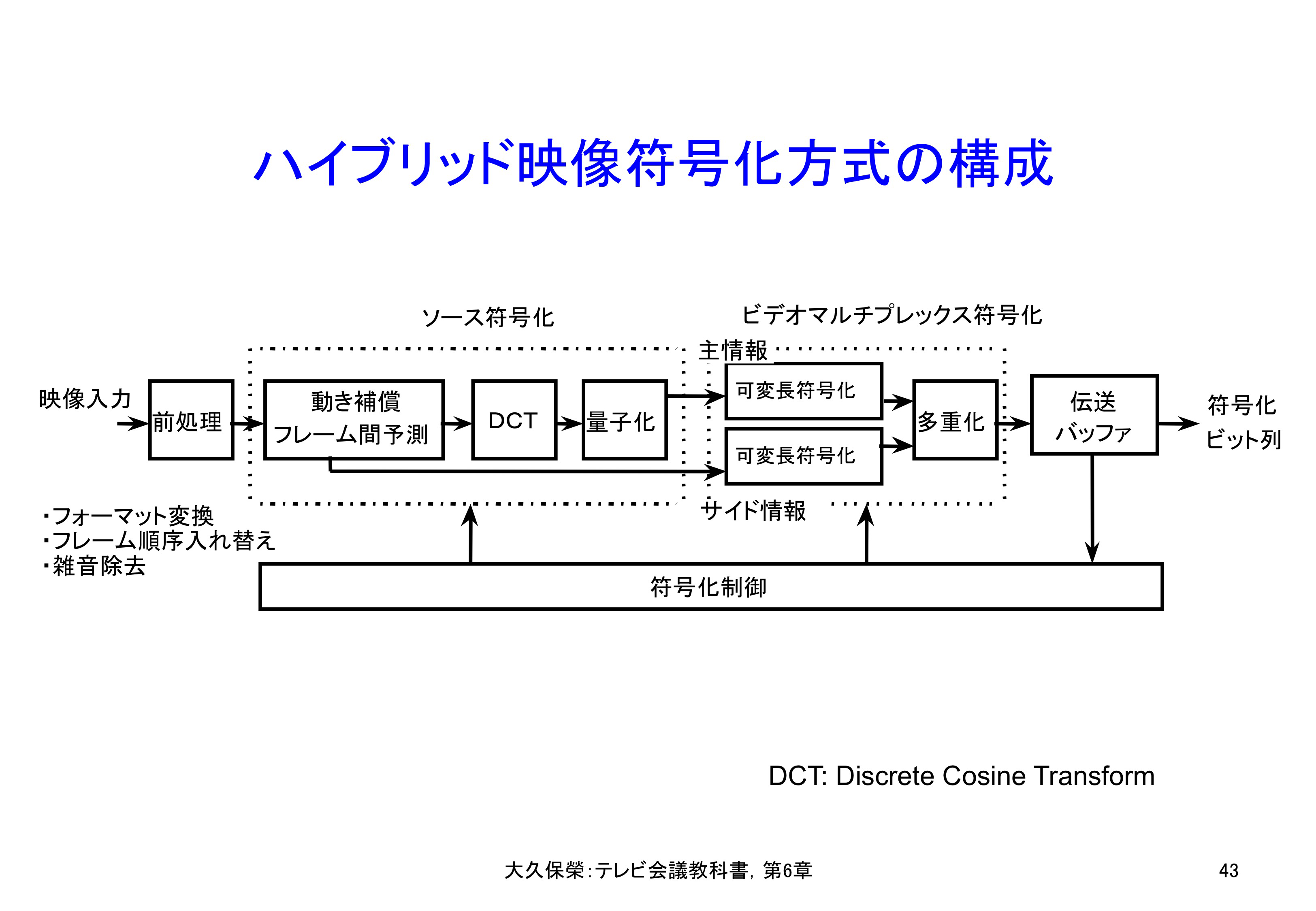
ソース符号化では,動き補償フレーム間予測誤差をDCT変換して画像に含まれる冗長な情報を除きます.ビデオマルチプレックス符号化では,ソース符号化で得られた結果の発生頻度に偏りのあることを利用して統計的な冗長度を除く可変長符号化を施し各種伝送情報を多重化します.伝送バッファは,画像の部分毎に情報発生量の異なる符号化結果を一定伝送速度で送り出すためのものです.符号化制御は,情報発生量を見ながら画像の部分毎に符号化パラメータを制御します.
まず,前処理回路において,時間・空間フィルタにより,入力映像信号をディジタル・フォーマットに変換し,あわせて雑音除去フィルタリングを行います.ソース符号化回路は動き補償フレーム間予測とDCTにより入力信号に含まれる冗長な情報を除き,残りの信号を一定の誤差の範囲内で量子化します.ビデオマルチプレックス符号化回路では,画像符号化の主情報とブロック属性などのサイド情報を可変長符号化した後,定められたデータ構造の符号列に多重化します.伝送バッファでは変動する情報発生を一定レートに平滑化します.符号化制御回路は,符号化アルゴリズムの中の要素をどのように使って,符号化画質を最良にしながら与えられたチャネルレートのビット列を発生するかを決定します.
このように生成された符号列は,アプリケーションによって,伝送チャネルに適した形に整えられます.例えば,IPネットワーク上の映像伝送ではRTP (Real-time Transport Protocol,第7.3.2項参照)パケットに包んで送ることになります.
9) 階層符号化(SVC, Scalable Video Coding)
音声符号化について第6.2.2項の6)で説明した階層符号化の概念は,映像符号化にも適用されます.スケーラブル(scalable)符号化あるいはスケーラビリティ(scalability)と呼ばれることもあります.スケーラブルとは環境に応じて拡張可能の意味で,具体的にはビットストリームの一部を捨てても復号器がそれなりの映像を再現できる機能です[6-41].
映像の階層符号化では,次の4種類のスケーラビリティが考慮されます.
- 空間スケーラビリティ-- 異なる空間解像度の映像を対象とします.例えばSDTVとHDTV
- 時間スケーラビリティ-- 異なる時間解像度の映像を対象とします.例えば60フレーム/秒の映像と30フレーム/秒の映像
- SNRスケーラビリティ-- 異なる符号化雑音の映像を対象とします
- 色解像度スケーラビリティ-- 異なる色解像度の映像を対象とします.例えば4:2:2スタジオ標準映像と4:2:0分配標準映像
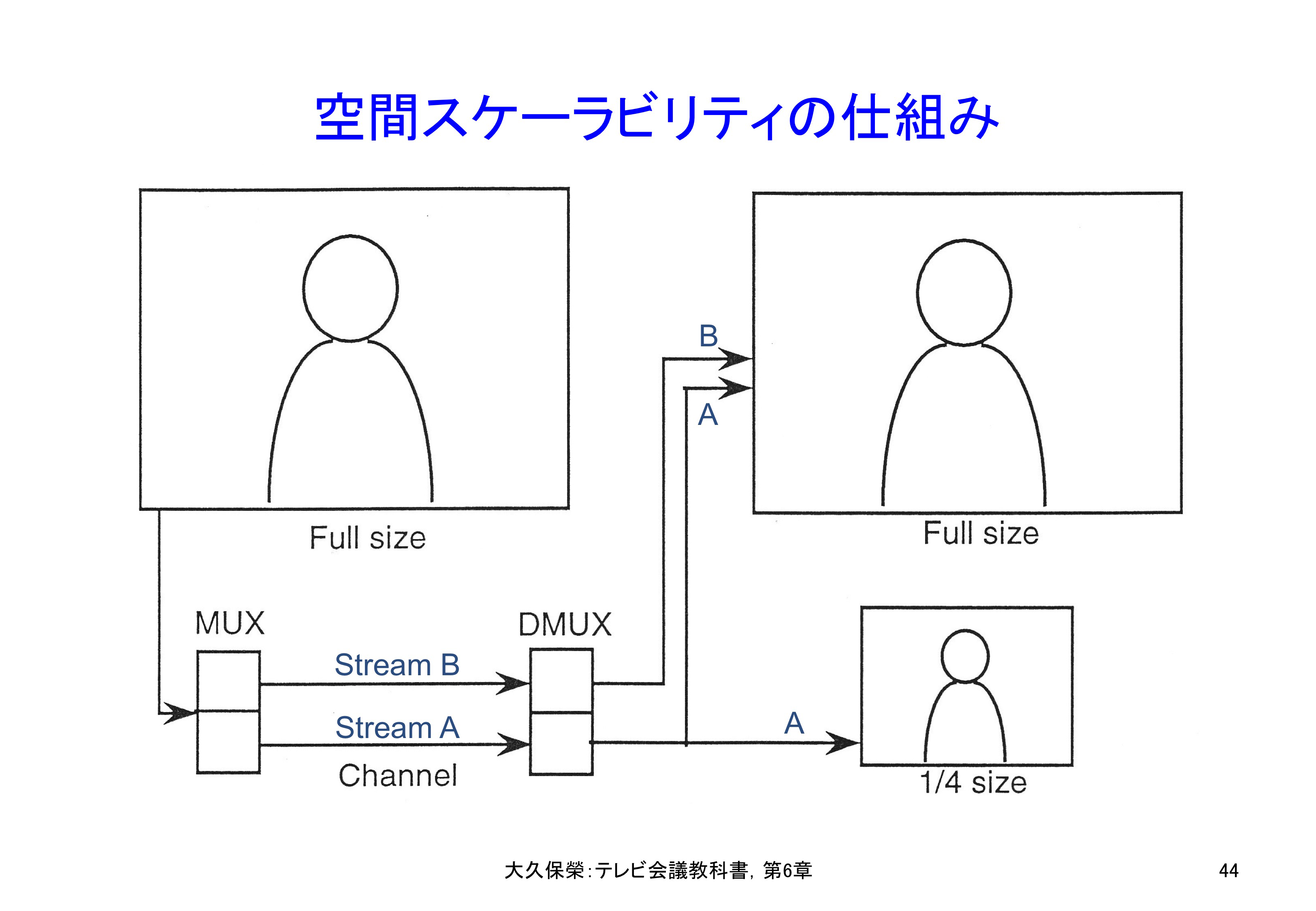
図6-44に空間スケーラビリティの仕組みを示します.送信側は2層構造になっていて基底層となる1/4解像度画面を符号化したストリームと,それからの差分の形で符号化し拡張層となるフル解像度画面のストリームに分けて送り出します.受信側では基底層ストリームのみを受信すれば1/4解像度画面が,基底層と拡張層の両方を受信すればフル解像度画面を再現することができます.一般に拡張層のみのストリームからは意味のある画像を再現することはできません.さらに用途によっては3層以上の階層符号化も用いられます.